Formel für den Abstand eines Punktes zu einer Geraden

Der Abstand eines Punktes zu einer Geraden im dreidimensionalen Raum lässt sich mit Hilfe des Vektorproduktes (Kreuzproduktes) berechnen.

Formel für den Abstand Punkt – Gerade im R³

Der Abstand des Punktes $P$ zu einer Geraden $g:\vec x=\vec a+t\cdot \vec u$ im dreidimensionalen Raum beträgt $d=\dfrac{|(\vec p-\vec a)\times \vec u|}{|\vec u|}$.

Da die Formel noch keinen Eingang in die gängigen Schulbücher und Formelsammlungen gefunden hat, begründe ich sie an dieser Stelle.

Dazu ergänzen wir zunächst die Gerade und den außerhalb liegenden Punkt zu einem Dreieck.

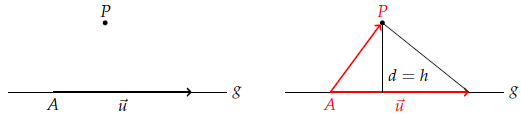
Beweis für Formel Abstand Punkt Gerade

Seinen Flächeninhalt können wir mithilfe des Vektorproduktes angeben: $A_{\Delta}=\tfrac 12\cdot |\overrightarrow{AP}\times \vec u|$.

Andererseits kennen wir aus der Mittelstufe die Formel $A_{\Delta}=\frac 12\cdot g\cdot h$. Die Höhe $h$ wiederum ist der Abstand $d$ des Punktes zur Geraden, die Grundseite $g$ die Länge des Richtungsvektors. Durch Einsetzen und Umformen erhalten wir:
$\begin{align*}\tfrac 12\cdot g\cdot h&=\tfrac 12\cdot |\overrightarrow{AP}\times \vec u|&&| \text{ ersetze } g=|\vec u|;h=d;\overrightarrow{AP}=\vec p-\vec a\\ \tfrac 12 \cdot |\vec u|\cdot d&=\tfrac 12\cdot |(\vec p-\vec a)\times \vec u|&& |\cdot 2:|\vec u|\\ d&=\dfrac{|(\vec p-\vec a)\times \vec u|}{|\vec u|}\end{align*}$

Gelegentlich zieht man den Nenner $|\vec u|$ in den Zähler zum Vektor $\vec u$ und nutzt die Schreibweise $\vec u_0=\dfrac{1}{|\vec u|}\cdot \vec u$ für den Einheitsvektor. Die Formel lässt sich dann zwar kompakter als $d=|(\vec p-\vec a)\times \vec u_0|$ schreiben, ist aber bei der konkreten Berechnung unbequemer.

Beispiele

Beispiel 1: Punkt gegeben, Abstand gesucht

Gesucht ist der Abstand des Punktes $P(10|5|7)$ von der Geraden $g\colon \vec x=\begin{pmatrix}-2\\1\\7\end{pmatrix}+s\begin{pmatrix}4\\1\\-3\end{pmatrix}$.

Lösung: Man berechnet zunächst $\overrightarrow{AP}=\vec p-\vec a=\begin{pmatrix}12\\4\\0\end{pmatrix}$ und damit das Kreuzprodukt $(\vec p-\vec a)\times \vec u=\begin{pmatrix}12\\4\\0\end{pmatrix}\times \begin{pmatrix}4\\1\\-3\end{pmatrix}=\begin{pmatrix}4\cdot (-3)-0\cdot 1\\0\cdot 4-12\cdot (-3)\\12\cdot 1-4\cdot 4\end{pmatrix}=\begin{pmatrix}-12\\36\\-4\end{pmatrix}$.

Damit erhält man für den Abstand $d=\dfrac{\sqrt{12^2+36^2+4^2}}{\sqrt{4^2+1^2+3^2}}=\sqrt{56}\approx 7{,}48\, \text{LE}$.

Das Verfahren ist also wesentlich schneller als das Lotfußpunktverfahren, hat aber den Nachteil, dass der Fußpunkt auf diese Weise nicht ermittelt wird. Da dies gelegentlich verlangt wird, muss man das andere Verfahren trotzdem beherrschen.

Das Verfahren lässt sich natürlich auch einsetzen, um den Abstand paralleler Geraden zu berechnen: Man wählt auf einer der Geraden einen Punkt – am einfachsten den Stützpunkt – und berechnet den Abstand dieses Punktes zur anderen Geraden.

Beispiel 2: Abstand gegeben, Parameter oder Punkt gesucht

Gegeben ist die Gerade $g:\vec x=\begin{pmatrix}1\\1\\-3\end{pmatrix}+s\begin{pmatrix}2\\2\\-1\end{pmatrix}$. Gesucht sind die Punkte der $y$-Achse, die von dieser Geraden 5 Längeneinheiten entfernt sind.

Lösung: Punkte auf der $y$-Achse sind von der Form $P(0|y|0)$. Wir berechnen zunächst wieder $\overrightarrow{AP}=\begin{pmatrix}0\\y\\0\end{pmatrix}-\begin{pmatrix}1\\1\\-3\end{pmatrix}=\begin{pmatrix}-1\\y-1\\3\end{pmatrix}$ und damit das Vektorprodukt $(\vec p-\vec a)\times \vec u=\begin{pmatrix}-1\\y-1\\3\end{pmatrix}\times \begin{pmatrix}2\\2\\-1\end{pmatrix}=\begin{pmatrix}(-y+1)-6\\6-1\\-2-(2y-2)\end{pmatrix}=\begin{pmatrix}-y-5\\5\\-2y\end{pmatrix}$.

Der Abstand soll $d=5$ betragen. Wir setzen in die Formel ein und lösen nach $y$ auf. Dabei benötigen wir zu Beginn eine binomische Formel und am Schluss die $pq$-Formel.

\[\begin{align*}\dfrac{\sqrt{(-y-5)^2+5^2+(-2y)^2}}{\sqrt{2^2+2^2+1^2}}&=5\\\dfrac{\sqrt{y^2+10y+25+25+4y^2}}{3}&=5&& |\cdot 3\\ \sqrt{5y^2+10y+50}&=15 &&|(\cdots)^2\\ 5y^2+10y+50&=225&&|-225\\5y^2+10y-175&=0&&|:5\\ y^2+2y-35&=0&&|pq\text{-Formel}\\ y_{1,2}&=-1\pm \sqrt{1^2+35}\\ y_1&=5\\y_2&=-7\end{align*}\]

Die beiden Punkte haben also die Koordinaten $P_1(0|5|0)$ und $P_2(0|-7|0)$.

Ist umgekehrt gefragt, welche Punkte der Geraden $g$ von der $y$-Achse den Abstand 5 haben, so stellt man die $y$-Achse als Gerade $h$ dar. Der Ursprung ist ein Stützvektor und muss als Nullvektor nicht notiert werden; die einfachste Wahl für den Richtungsvektor ist $\begin{pmatrix}0\\1\\0\end{pmatrix} \;\Rightarrow\; h:\vec x=t\begin{pmatrix}0\\1\\0\end{pmatrix}$. Der Punkt $P$ der Geraden $g$ wird allgemein in der Form $P(1+2s|1+2s|-3-s)$ geschrieben.

Man erhält $\overrightarrow{AP}\times \vec u=\begin{pmatrix}1+2s\\1+2s\\-3-s\end{pmatrix}\times \begin{pmatrix}0\\1\\0\end{pmatrix}=\begin{pmatrix}3+s\\0\\1+2s\end{pmatrix}$. Rechnet man wie oben weiter, so erhält man $s_1=1$ und $s_2=-3$. Setzt man diese Werte in $P$ ein, so erhält man die Koordinaten $P_1(3|3|-4)$ und $P_2(-5|-5|0)$ der gesuchten Punkte.

Übungsaufgaben

Teilen Info Bei den "Teilen"-Schaltflächen handelt es sich um rein statische Verlinkungen, d.h. sie senden von sich aus keinerlei Daten an die entsprechenden sozialen Netzwerke. Erst wenn Sie einen Link anklicken, öffnet sich die entsprechende Seite.

↑

Abstandsberechnungen im R³

Beispiele, Erklärungen

Punkt – Punkt
Punkt – Gerade: Lotfußpunktverfahren mit Hilfsebene
Punkt – Gerade: Lotfußpunktverfahren mit laufendem Punkt
Punkt – Gerade: Formel
Punkt – Ebene: Lotfußpunktverfahren
Punkt – Ebene: Formel
Windschiefe Geraden: Formel
Windschiefe Geraden: Lotfußpunkte mit laufenden Punkten
Windschiefe Geraden: Lotfußpunkte mit Hilfsebene

Aufgaben

Punkt – Punkt (Lösungen)
Punkt – Gerade: Lotfußpunktverfahren (Lösungen)
Punkt – Gerade: Formel (Lösungen)
Punkt – Ebene: Lotfußpunktverfahren (Lösungen)
Punkt – Ebene: Formel (Lösungen)
Windschiefe Geraden: Formel (Lösungen)
Windschiefe Geraden: Lotfußpunkte (Lösungen)