Abstand windschiefer Geraden: Lotfußpunktverfahren mit Hilfsebene

Die Formel für den Abstand windschiefer Geraden liefert nur die minimale Entfernung, gibt aber keine Auskunft darüber, in welchen Punkten der Geraden der Abstand angenommen wird. Die Fußpunkte erhält man mit einem Lotfußpunktverfahren.

Auf dieser Seite arbeiten wir mit der Methode der Hilfsebene. Das Verfahren mit laufenden Punkten finden Sie hier.

Vorgehensweise: Abstand windschiefer Geraden mit einer Hilfsebene

Gegeben seien zwei windschiefe Geraden $g\colon \vec x=\vec p+r\,\vec u$ und $h\colon \vec x=\vec q+s\,\vec v$. Die Punkte $F_g$ und $F_h$ seien die Fußpunkte des gemeinsamen Lotes. Die hellgrauen Hilfsebenen sollen nur das räumliche Vorstellungsvermögen unterstützen und haben für die Rechnung keine Bedeutung.

Abstand windschiefer Geraden: Lotfußpunktverfahren mit Hilfsebene

Die Hilfsebene $E_g$ wird so gewählt, dass sie die Gerade $g$ enthält und der zweite Spannvektor (Richtungsvektor) $\vec n$ auf den Richtungsvektoren beider Geraden senkrecht steht.

Man bestimmt einen Vektor $\vec n$, der auf beiden Richtungsvektoren senkrecht steht, und konstruiert eine Hilfsebene $E_g\colon \vec x=p+r\,\vec u+t\,\vec n$.
Man berechnet den Schnittpunkt (Lotfußpunkt) $F_h$ der Ebene $E_g$ mit der Geraden $h$. Anschließend berechnet man den Lotfußpunkt $F_g$.
Der Abstand der windschiefen Geraden beträgt $d=\left|\overrightarrow{F_gF_h}\right|$.

Beispiel

Aufgabe: Gegeben sind die windschiefen Geraden $g\colon \vec x=\begin{pmatrix}-7\\2\\-3\end{pmatrix}+r\,\begin{pmatrix}0\\1\\2\end{pmatrix}$ und $h\colon \vec x=\begin{pmatrix}-3\\-3\\3\end{pmatrix}+s\,\begin{pmatrix}1\\2\\1\end{pmatrix}$. Gesucht sind der Abstand der Geraden und die Fußpunkte des gemeinsamen Lotes.

Lösung:

Schritt 1: Wir bestimmen einen Normalenvektor. Ich verwende das Kreuzprodukt, da es mittlerweile recht weit verbreitet ist. Sie können natürlich auch mithilfe der Skalarprodukte ein Gleichungssystem aufstellen.
$\vec u\times \vec v = \begin{pmatrix}0\\1\\2\end{pmatrix} \times \begin{pmatrix}1\\2\\1\end{pmatrix}= \begin{pmatrix}1-4\\2-0\\0-1\end{pmatrix} = \begin{pmatrix}-3\\2\\-1\end{pmatrix}\quad \text{wähle }\vec n=-\, \vec u\times \vec v=\begin{pmatrix}3\\-2\\1\end{pmatrix}$

Das Ergebnis des Vektorprodukts kann natürlich auch ohne Änderung verwendet werden. Ich bevorzuge einen Vektor mit möglichst wenigen Minuszeichen.

Mit diesem Vektor erstellen wir die Hilfsebene. Aufgrund der gewählten Konstruktion ist es sinnvoll, die Parameterform beizubehalten und die Ebene nicht in die Koordinatenform oder Normalenform umzuwandeln.

Hilfsebene $E_g\colon \vec x=\begin{pmatrix}-7\\2\\-3\end{pmatrix}+r\,\begin{pmatrix}0\\1\\2\end{pmatrix}+t\,\begin{pmatrix}3\\-2\\1 \end{pmatrix}$

Schritt 2: Den Schnittpunkt berechnen wir, indem wir die Ebenengleichung mit der Gleichung von $h$ gleichsetzen:

$\begin{pmatrix}-7\\2\\-3\end{pmatrix}+r\,\begin{pmatrix}0\\1\\2\end{pmatrix}+t\,\begin{pmatrix}3\\-2\\1 \end{pmatrix} = \begin{pmatrix}-3\\-3\\3\end{pmatrix}+s\,\begin{pmatrix}1\\2\\1\end{pmatrix}$

Wir sortieren und stellen dabei das Gleichungssystem auf. Hier wird es von Hand gelöst; einfacher ist es natürlich, wenn Sie es mit dem Taschenrechner lösen dürfen.

$\begin{alignat*}{5} & \text{I} & && \, 3t && \, - \, s &\,= 4 &&\hspace{2em} |\to \text{II}_a\\ & \text{II} & r \, && - \, 2t && \, - \, 2s &\,= -5 &&\hspace{2em} |\to \text{I}_a\\ & \text{III} &\hspace{2em} 2r \, && + \, t && \, - \, s &\,= 6 &&\hspace{2em} |\text{ III}-2\cdot \text{II}\\ \text{}\\ & \text{I}_a & r \, && - \, 2t && \, - \, 2s&\,=-5\\ & \text{II}_a & && \, 3t && \, - \, s &\,=4\\ & \text{III}_a & && \, 5t && \, + \, 3s &\,= 16 &&\hspace{2em} |\text{ III}_a+3\cdot\text{II}_a\\ \text{}\\ & \text{I}_a & r \, && - \, 2t && \, - \, 2s &\,= -5 \\ & \text{II}_a & && \, 3t && \, - \, s &\,= 4 \\ & \text{III}_b & && \, 14t && &\,= 28 &&\hspace{2em} |:14\\ & & && \, t && &\,= 2\\ \text{}\\ & t \text{ in II}_a & \, && \, 6 && \,- \, s&\,= 4 &&\hspace{2em} |-6\\ & & && && \,- \, s&\,= -2 &&\hspace{2em} |:(-1)\\ & & && && s&\,= 2\\ \text{} \\ & s,t \text{ in I}_a & r\, && -\, 4 && \,- \, 4&\,= -5 &&\hspace{2em} |+8\\ & & r\, && && &\,= 3\\ \end{alignat*}$

Zur Berechnung der Koordinaten des Fußpunktes $F_h$ setzen wir $s=2$ in die zugehörige Geradengleichung ein:

$\overrightarrow{f_h}=\begin{pmatrix}-3\\-3\\3\end{pmatrix}+2\cdot\begin{pmatrix}1\\2\\1\end{pmatrix} = \begin{pmatrix}-1\\1\\5\end{pmatrix}\quad F_h(-1|1|5)$

Bevor wir fortfahren, schauen wir uns unsere Ergebnisse in der Grafik an. Achten Sie dabei auf die Vielfachen der Richtungs- bzw. Spannvektoren:

Der Parameter $s$ gibt an, wie oft man auf der Geraden $h$ den Richungsvektor aneinanderhängt. In diesem Fall müssen wir von $Q$ aus zweimal (wegen $s=2$) den Richungsvektor $\vec v$ ablaufen, um zum Schnittpunkt bzw. Fußpunkt $F_h$ zu gelangen.
Der Parameter $r=3$ gibt an, wie oft man den Vektor $\vec u$ läuft, also den Richtungsvektor von $g$ bzw. den ersten Spannvektor der Hilfsebene $E_g$.
Der Parameter $t=2$ gibt an, wie oft man den zu beiden Geraden senkrechten Vektor $\vec n$ läuft, also den zweiten Spannvektor von $E_g$.

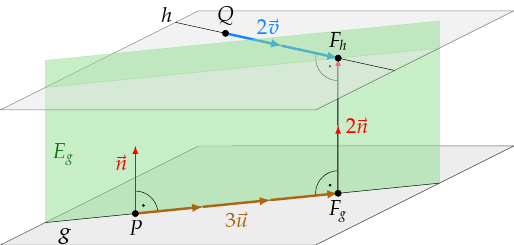
Abstand windschiefer Geraden: Zahlenbeispiel für Hilfsebene

Wenn wir $E_g$ in Koordinatenform verwandelt hätten, hätten wir jetzt nur die Koordinaten von $F_h$ und müssten eine weitere Rechnung anschließen, um auch den zweiten Fußpunkt zu bestimmen. Aufgrund der Wahl der Spannvektoren der Ebene haben wir jedoch indirekt auch den Fußpunkt $F_g$ ermittelt: wir müssen nur noch $r=3$ in die zugehörige Geradengleichung einsetzen.

$\overrightarrow{f_g}=\begin{pmatrix}-7\\2\\-3\end{pmatrix}+3\cdot\begin{pmatrix}0\\1\\2\end{pmatrix} = \begin{pmatrix}-7\\5\\3\end{pmatrix}\quad F_g(-7|5|3)$

Schritt 3: Für den Abstand berechnen wir zunächst den Verbindungsvektor und anschließend dessen Länge:

$\overrightarrow{F_gF_h}=\overrightarrow{f_h}-\overrightarrow{f_g}=\begin{pmatrix}-1\\1\\5\end{pmatrix} - \begin{pmatrix}-7\\5\\3\end{pmatrix} = \begin{pmatrix}6\\-4\\2\end{pmatrix}$
$d(g,h)=\left|\overrightarrow{F_gF_h}\right|=\sqrt{6^2+(-4)^2+2^2}=\sqrt{56}\approx 7{,}48\text{ LE}$

Alternativ können Sie den Verbindungsvektor auch über die Beziehung $\overrightarrow{F_gF_h}=t\cdot \vec n=2\cdot \begin{pmatrix}3\\-2\\1\end{pmatrix} = \begin{pmatrix}6\\-4\\2\end{pmatrix}$ ermitteln.

Ergebnis: Die kürzeste Verbindung zwischen den Geraden besteht für die Punkte $F_g(-7|5|3)$ auf $g$ und $F_h(-1|1|5)$ auf $h$. Für diese Punkte beträgt die Entfernung etwa 7,48 Längeneinheiten.

Übungsaufgaben

Teilen Info Bei den "Teilen"-Schaltflächen handelt es sich um rein statische Verlinkungen, d.h. sie senden von sich aus keinerlei Daten an die entsprechenden sozialen Netzwerke. Erst wenn Sie einen Link anklicken, öffnet sich die entsprechende Seite.

↑

Abstandsberechnungen im R³

Beispiele, Erklärungen

Punkt – Punkt
Punkt – Gerade: Lotfußpunktverfahren mit Hilfsebene
Punkt – Gerade: Lotfußpunktverfahren mit laufendem Punkt
Punkt – Gerade: Formel
Punkt – Ebene: Lotfußpunktverfahren
Punkt – Ebene: Formel
Windschiefe Geraden: Formel
Windschiefe Geraden: Lotfußpunkte mit laufenden Punkten
Windschiefe Geraden: Lotfußpunkte mit Hilfsebene

Aufgaben